The new minimum capital requirements for market risk in the trading book set out by Basel’s Fundamental Review of the Trading Book (FRTB) are approaching fast. In this blog, we discuss FRTB’s impact for positions in non-callable mortgage-backed bullet bonds (so-called RTL bonds1) of which Danish banks hold about 400bn DKK in notional. We estimate capital requirements to increase somewhat less than the 30-40% target increase set by the Basel committee.
As part of developing the Basel III framework, the Basel Committee on Banking Supervision initiated the Fundamental Review of the Trading Book (FRTB). Several years later, the outcome is a new set of global standards for calculating minimum capital requirements for market risk in the trading book. The EU plans to implement the standards for European credit institutions in the Capital Requirements Regulation/Directive (CRR/CRD) in the coming years.
At the time of writing, Danish banks are required to report minimum capital requirements under the standardised approach (SA-FRTB) by the end of the first quarter of 2021 when the notional of the trading book is higher than 500M EUR or when the trading book comprises more than 10 pct. of the bank’s total assets2.
In this blog, we outline how the SA-FRTB guidelines should be implemented on Danish RTL bonds. To keep things simple, we calculate SA-FRTB minimum capital requirements for non-hedged, single bond portfolios. Compared to current Danish legislation we find that the highest increase in required capital is 27% and is imposed on the longest RTL bonds. This is somewhat less than indicated by the Basel Committee and for medium-term bonds, the capital requirements actually decline.
The new way of dealing with issuer specific spread risk (the CSR risk class) is the main driver for increasing capital needs, but a new method of capitalizing jump-to-default risk partially offsets the increase. Hence, the impact of FRTB on RTL bonds of which Danish banks hold about 400bn DKK in notional according to Danmarks Nationalbank, appears to be limited which is probably good news for the banks. However, FRTB may have a larger impact on floating rate and callable mortgage bonds for which convexity and vega risk should be included. This will be discussed in an upcoming blog. The final impact of FRTB will also depend on the overall hedge positions taken by the bank.
You may also want to read
- An introduction to FRTB for Danish bonds
- How will FRTB affect required capital for RTL bonds?
- How will FRTB affect required capital for floating rate notes?
A summary of the Standardised Approach
The Standardised Approach results in a capital requirement. It is a simple sum of three components
- \(K_{SBM}\) : Capital requirement under the sensitivity-based method
- \(K_{DRC}\) : Capital requirement of default risk capital
- \(K_{RRAO}\) : Capital requirement of residual risk add on
That is $$K_{SA-FRTB}=K_{SBM}+K_{DRC}+K_{RRAO}$$
SBM categorizes trading book market risks in seven risk classes. In the fact box, we provide a high-level overview of SBM. DRC capitalizes jump-to-default risks not capitalized by credit spread shocks under SBM. RRAO captures exotic risks not included in the other two components.
|
Fact box - The sensitivity-based method The starting point of the SBM is the three risk measures, delta, curvature and vega. Delta measures first order changes in value, whereas curvature captures any non-linearities, e.g. embedded options. Vega measures volatility risk. Each risk measure defines a list of risk factors and corresponding risk weights. Let \(k\) be such a risk factor, \(s_{k}\) the net sensitivity in the trading book for that risk factor and \(RW_{k}\) the corresponding risk weight. The weighted sensitivity, \(WS_{k}\), is given as $$WS_{k}=RW_{k}\cdot s_{k}$$ It quantifies how much the value of the instruments in the trading book changes in accordance with a change in the underlying risk factor. Note that \(RW_{k}\) specifies how much the risk factor is expected to change in an adverse scenario. The weighted sensitivities are grouped together based on instrument characteristics, e.g. currency or sector. These groups are called risk buckets. The aggregated capital requirement of a risk bucket, \(K_{b}\) where \(b\) is a bucket, is calculated using bucket-correlations, \(\rho_{k l}\) , prescribed by the Basel framework $$K_{b}=\sqrt{\Bigl(\sum_{k}\sum_{l} \rho_{k l}WS_{k}WS_{l}\Bigl)^+}$$ The risk buckets are again aggregated according to prescribed between-bucket-correlations to derive the capital requirement in a risk class. The total capital requirement for a risk class is the simple sum of all three risk measures. $$K_{RiskClass}=K_{RiskClass}^{Delta}+K_{RiskClass}^{Vega}+K_{RiskClass}^{Curvature}$$ Finally, \(K_{SBM}\) is the sum of all \(K_{RiskClass}\). There are seven risk classes in total, we are interested in General Interest Rate Risk (GIRR) and Credit Spread Risk (CSR).
CSR*: Securitisations, non-correlation trading portfolio (non-CTP) CSR**: Securitisations, correlation trading portfolio (CTP)
|
Setting the stage for FRTB calculations
Our first task in calculating capital requirements under SA-FRTB is to identify the relevant risk factors. They are listed in Basel (Jan 2019) 21.8 and 21.9, but it can be unclear how to apply those guidelines to some of the more complex bonds in the Danish market. However, RTL bonds are pretty straight-forward. In Table 1, we list the FRTB risk factors for GIRR and CSR relevant for Danish RTL bonds.
| CLASS | MEASURE | BUCKET | FACTORS | REFERENCE |
|---|---|---|---|---|
| GIRR | Delta | Currency | Risk-free yield curve @ 0.25, 0.5, 1, 2, 3, 5, 10, 15, 20, 30Y | 21.8.(1) |
| CSR | Delta | Rating and sector | Issuer credit spread curve @ 0.5, 1, 3, 5, 10Y | 21.9.(1) |
Table 1: Risk factors defined by FRTB. Reference paragraphs refer to Basel (Jan. 2019).
The coupon payments of RTL bonds are fixed, and the bonds are non-callable and therefore exempt from curvature and vega capitalization3.
The risk-free yield curve is chosen as the Danish CITA-curve, and in our calculations the credit spread is defined as a complete issuer spread curve to the risk-free yield curve. The issuer spread curves are estimated on top of the CITA curve. The samples consist entirely of RTL bonds.
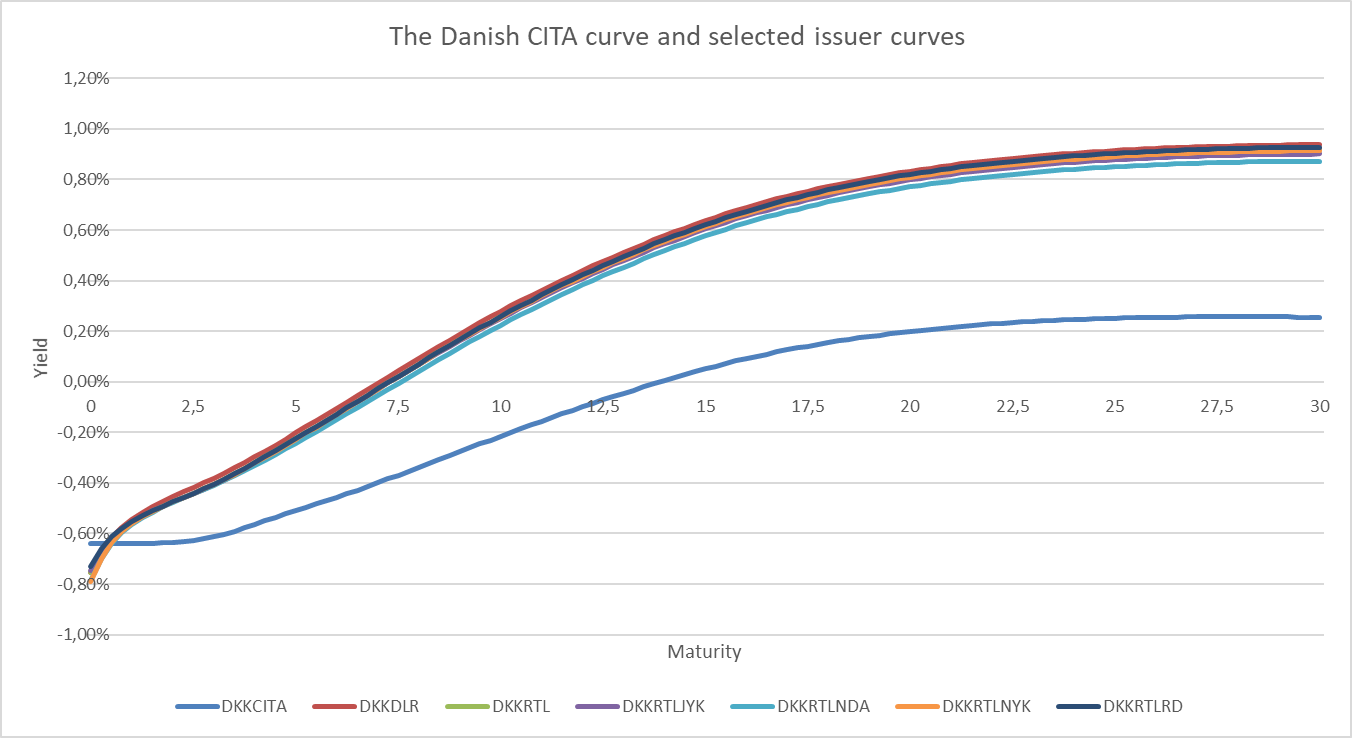
Figure 1: Credit spread curves for Danish covered bonds are all at the same level on 21 October 2019.
Shocking the yield curves
As shown in Table 1, we need to shock two curves in the FRTB calculations of RTL bonds. When the risk-free curve is shifted, the credit spread must be kept fixed. Figure 2 illustrates a bucket shift to the risk-free curve, i.e. the shifts to be applied in the GIRR case.
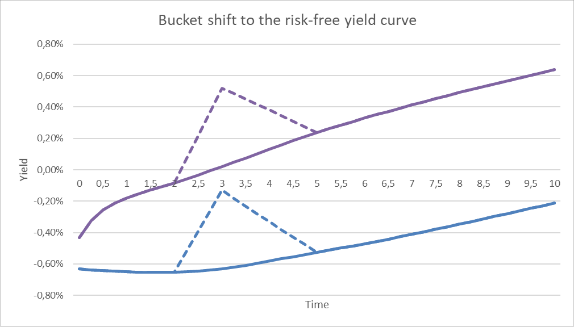
Figure 2: A bucket shift to the 3Y tenor for the risk-free yield curve (blue) also leads to a shift in the issuer credit spread curve (purple). This represents the GIRR case.
Figure 3 illustrates when the issuer credit spread curve is shifted alone, i.e. the CSR shift to be applied.
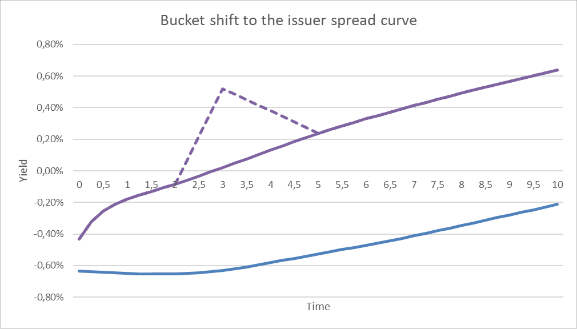
Figure 3: A bucket shift to the 3Y tenor for the issuer credit spread curve (purple). The risk-free curve (blue) is unaffected. This represents the CSR case.
Since RTL bonds are priced by discounting a fixed cash flow on the credit curve, the GIRR and CSR sensitivities will be very similar.
FRTB does not specify how the bucket shifts should be implemented, and as we have shown in a previous blog4, the standard triangular bucket shifts do not add up to the duration of the bond. Therefore, we use the methodology explained in said blog ensuring that the delta vector sums to the bond duration.
SA-FRTB applied to a single RTL bond
In the following sections, we have selected 1 RD T RTL 2023 (DK0009295065) to illustrate the FRTB calculations in a very simple setup. Our portfolio consists only of a single bond with a notional of 100.
Delta GIRR
Using the methodology explained in the previous sections, we are able to calculate a vector of risk factor sensitivities for our test bond and apply the sensitivities to the SA-FRTB guidelines. Table 2 shows the calculations.
| KEY RATE | SENSITIVITY (\(s_k\)) | RISK WEIGHT (\(RW_{k}\)*) | WEIGHTED SENSITIVTY (\(WS_{k}\)) |
|---|---|---|---|
| 0.25 | 0.0010 | 1.7% / \(\sqrt{2}\) | 0.0012 |
| 0.50 | 0.0036 | 1.7% / \(\sqrt{2}\) | 0.0043 |
| 1 | 0.0080 | 1.6% / \(\sqrt{2}\) | 0.0091 |
| 2 | 0.0206 | 1.3% / \(\sqrt{2}\) | 0.0189 |
| 3 | 2.7607 | 1.2% / \(\sqrt{2}\) | 2.3425 |
| 5 | 0.8030 | 1.1% / \(\sqrt{2}\) | 0.6246 |
Table 2: GIRR delta sensitivities for “1 RD T RTL 2023” on 21 October 2019. The sensitivities are expressed for 1 pct. bucket shifts. * Risk weights are specified in Basel (Jan 2019) 21.42. They are divided by \(\sqrt{2}\) because of European Parliament (2019/876) Article 325ae pt. 3. Due to the bond maturity, key rates for maturities above 5 years are zero and omitted.
The bucket grouping variable in GIRR is the currency, and the capital requirement is calculated using the equation in the fact box and the correlation matrix5. We only consider the normal correlation scenario. We need to evaluate \(\sum_{k}\sum_{l} \rho_{k l}WS_{k}WS_{l}\) where \(k\) and \(l\) runs through the risk factors which in this example are the ten key rates of DKKCITA. Our portfolio only consists of one bond, so there are no other risk buckets in play.
$$K_{GIRR}=K^{Delta}_{GIRR, DKK}=\sqrt{\Bigl(\sum_{k}\sum_{l} \rho_{k l}WS_{k}WS_{l}\Bigl)^+}=2.9837$$
As a side note, we mention that the correlation matrix is constructed in such a way that it can produce negative numbers for certain \(WS\) vectors, i.e. the matrix is not positive semidefinite. This is not usual behavior for correlation matrices and necessitates the floor of zero written as \((\cdot)^+\).
Delta CSR
The CSR delta is calculated in a similar fashion. The risk buckets in CSR are sector and rating and Danish mortgage bonds fall into sector category 8 (covered bonds)6. The risk weights for covered bonds are provided in FRTB as 1,5%, but in this blog we use the proposed risk weight of CRR27 which is 1%.
| KEY RATE | SENSITIVITY (\(s_k\)) | RISK WEIGHT (\(RW_{k}\)) | WEIGHTED SENSITIVITY (\(WS_{k}\)) |
|---|---|---|---|
| 0.5 | 0.0045 | 1% | 0.0045 |
| 1 | 0.0183 | 1% | 0.0183 |
| 3 | 2.7710 | 1% | 2.7710 |
| 5 | 0.8030 | 1% | 0.8030 |
Table 3: CSR delta sensitivities for “1 RD T RTL 2023” on 21 October 2019. The sensitivities are expressed for 1 pct. bucket shifts. Due to the bond maturity, key rates for maturities above 5 years are zero and omitted.
The weighted sensitivities in Table 3 are applied to the provided correlations. The single bond portfolio contains only one issuer name, so the correlations are all 0.65, and the CSR capital requirement is
$$K_{CSR}=K^{Delta}_{CSR, covBond, AAA}=\sqrt{\Bigl(\sum_{k}\sum_{l} \rho_{k l}WS_{k}WS_{l}\Bigl)^+}=3.3648$$
Hence, the total SBM capital requirement is
$$K_{SBM}=K^{Delta}_{GIRR}+K^{Delta}_{CSR}=6.3485$$
Default Risk Capital (DRC)
Calculating DRC in the standardised approach8 is a manageable task – especially in our case with a single bond portfolio. LGD (loss given default) is 25% for covered bonds and the risk weight for AAA-rated bonds is 0.5%. On the calculation date, “1 RD T RTL 2023” has a market price of 104.938.
$$DRC=(Notional \cdot LGD_{CovBond}+P\& L) \cdot RW_{AAA}\\=(100 \cdot 0.25 + 4.938) \cdot 0.005\qquad \qquad \ \\=0.1497 \ \qquad \ \qquad \qquad \ \qquad \qquad \quad \quad$$
The total SA-FRTB capital requirement is
$$K_{SA-FRTB}=K_{SBM}+K_{DRC}+K_{RRAO}=6.3485+0.1497+0=6.4982$$
Comparison with the current capital charges
Under current capital requirement regulation, general interest risk capitalization must be calculated using the duration-based method9 specified in CRR. The spread risk is a pillar II capital requirement, and for mortgage bonds the Danish regulator, Finanstilsynet, advises that the spread is shocked by a minimum of 50 bps. To determine default risk, the specific risk component in CRR should be used according to Finanstilsynet (2019) section 6.4.1. We have summarized current and FRTB capital requirements in Table 4.
| RISK TYPE | FRTB | CURRENT |
|---|---|---|
| Interest rate risk | GIRR | General |
| Spread risk | CSR | Pillar II |
| Default risk | DRC | Specific risk |
Table 4: The three types of risk associated with Danish mortgage bonds under both FRTB and current legislation.
We start with the general interest rate risk. The bond from the previous section, “1 RD T RTL 2023”, has a price of 104,938 and a modified duration of 3,3971 on 21 October 2019. The duration places the bond in zone two with a risk weight of 0.85% such that
$$DW_{CRR}=ModDuration \cdot Price \cdot RiskWeight = 3.0301$$
where \(DW_{CRR}\) is the duration-weighted capital requirement for the exposure. Since the portfolio only consists of one bond, the match algorithm of article 340 can be omitted.
The credit spread risk key figure for “1 RD T RTL 2023” on the calculation date is 3,5908. We assume a notional of 100 and calculate the pillar II spread risk capitalization for mortgage bonds as \(SpreadRisk \cdot 50bps\) which becomes 1.7954.
The specific risk under CRR is just a time-to-maturity dependent risk-weight multiplied by the value of the position: \(104.938 \cdot 0.016=1.6790\) .
Combined, “1 RD T RTL 2023” has a capital requirement of 6.5045 in the current regime. This is actually a little bit higher than the SA-FRTB capital requirement. The unexpected decrease in required capital occurs because the specific risk component is much higher than DRC.
So, what is the impact of FRTB?
We consider the full range of RTL bonds with different maturities and hence durations. The bonds are listed in Table 5.
| ISIN | BOND NAME | MATURITY DATE | OUTSTANDING AMOUNT | DURATION (PV01) |
|---|---|---|---|---|
| DK0009294761 | 1 RD T RTL 2020 | 2020-04-01 | 43.07 | 0.4496 |
| DK0009294845 | 1 RD T RTL 2021 | 2021-04-01 | 48.33 | 1.4954 |
| DK0009294928 | 1 RD T RTL 2022 | 2022-04-01 | 69.98 | 2.5281 |
| DK0009295065 | 1 RD T RTL 2023 | 2023-04-01 | 41.58 | 3.5969 |
| DK0009295149 | 1 RD T RTL 2024 | 2024-04-01 | 31.31 | 4.6491 |
| DK0009295222 | 1 RD T RTL 2025 | 2025-04-01 | 2.96 | 5.6997 |
| DK0009295305 | 1 RD T RTL 2026 | 2026-04-01 | 3.05 | 6.7480 |
| DK0004602570 | 1 RD T RTL 2027 | 2027-04-01 | 2.72 | 7.7590 |
| DK0009515363 | 1 NYK H RTL 2028 | 2028-01-01 | 1.59 | 8.5840 |
| DK0004607538 | 1 RD T RTL 2029 | 2029-04-01 | 1.52 | 9.7637 |
Table 5: RTL bonds in the Danish market with varying maturity dates. Outstanding is in billion DKK. Durations are calculated on 21 October 2019.
For each bond, we perform the capital requirement calculations as shown above. Figure 4 sums up the results. The largest increase is observed for the 2029 bond which is subject to a 27% increase in required capital. Surprisingly, the capital impact for “1 RD T RTL 2022” and “1 RD T RTL 2023” is negative. General interest rate risk capital is roughly unchanged. The CSR capital charge is about 80% higher than the current pillar II spread risk capital charge imposed by the Danish regulator, but the default risk capital charge is on the other hand reduced.
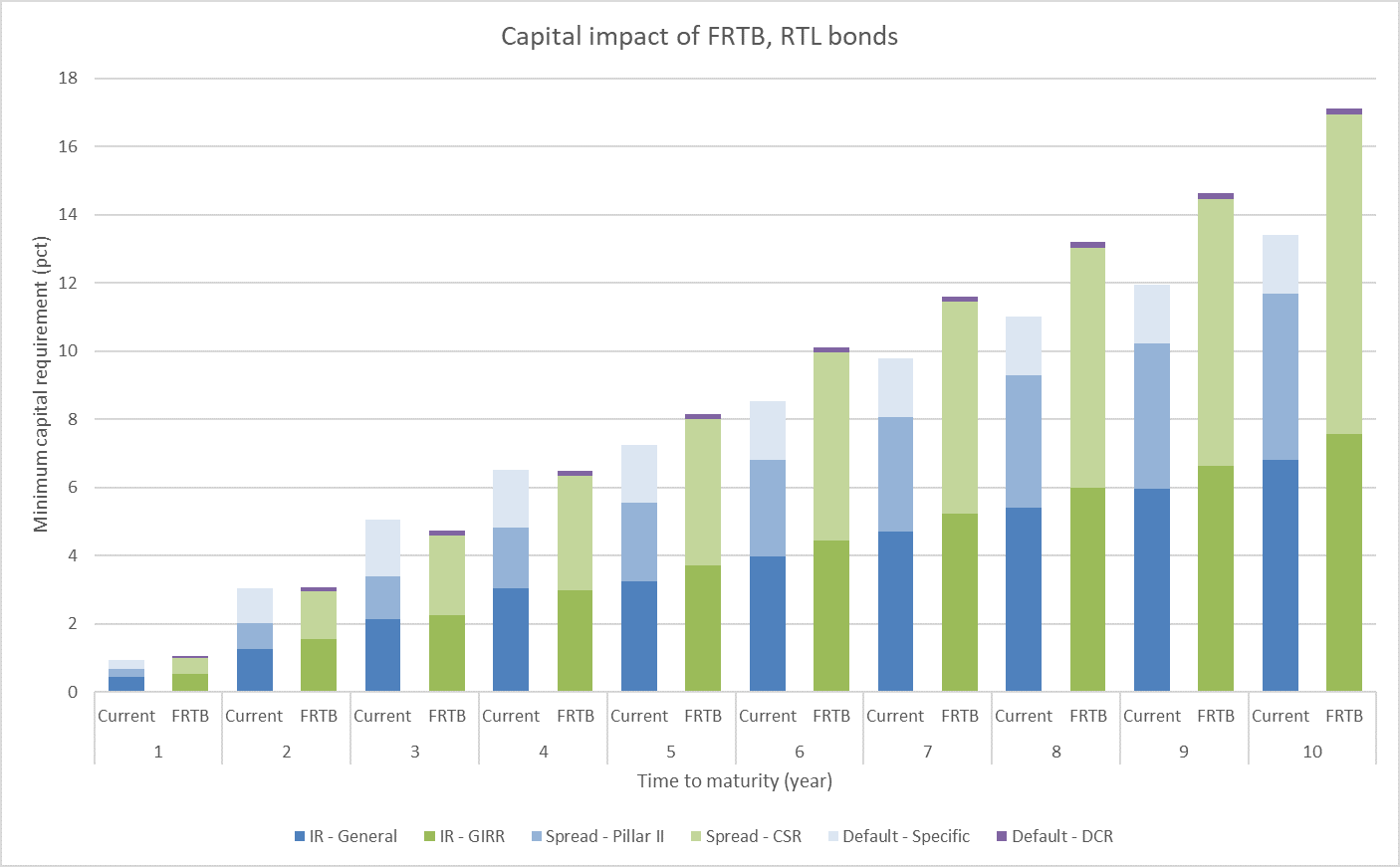
Figure 4: Estimated capital impact of RTL bonds for Danish banks. For each maturity segment, the largest RTL bond series is chosen. We estimate that the 3Y and 4Y bond will be subject to a smaller capital charge under the new framework.
The capital increase target by the Basel committee is 30-40%, but the reader should keep in mind that we have compared the new framework with the current Danish implementation. If we exclude the specific risk and DRC components the capital impact is very close to 40% for the entire list of bonds.
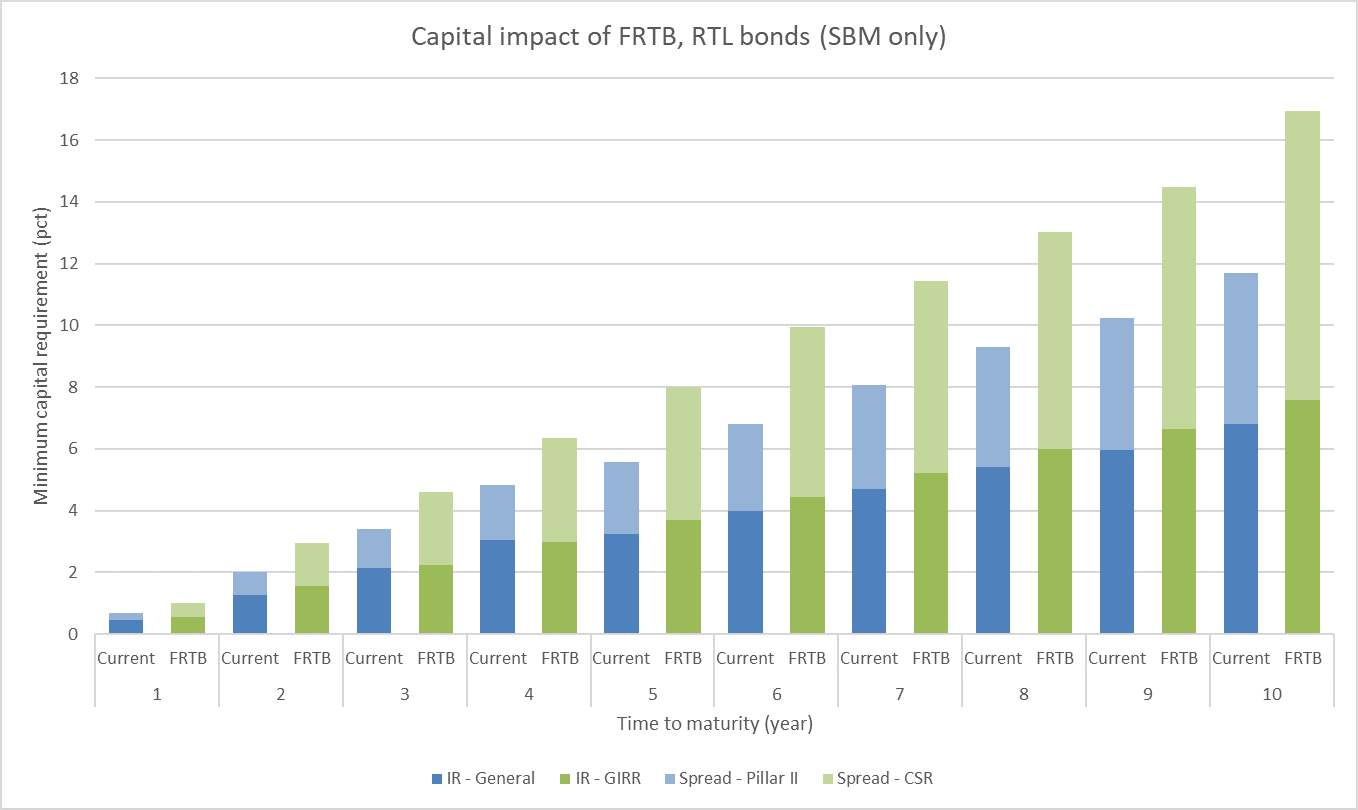
Figure 5: Estimated capital impact of RTL bonds for Danish banks. Only interest rate and spread risk are selected.
Issuer diversification reduces the CSR charge
SA-FRTB recognizes an issuer diversification effect in the CSR capital charge. The correlation between spread risk factors of different bond issuers is 0.35. To investigate the implication of this capital discount, we look at the five largest RTL series maturing in 2023.
| ISIN | BOND NAME | MATURITY DATE | OUTSTANDING AMOUNT | DURATION (PV01) |
|---|---|---|---|---|
| DK0002041029 | 1 NDA 2 RTL 2023 | 2023-10-01 | 9.82 | 4.1225 |
| DK0006345301 | 1 DLR B RTL 2023 | 2023-10-01 | 8.38 | 4.1105 |
| DK0009295065 | 1 RD T RTL 2023 | 2023-04-01 | 41.32 | 3.5909 |
| DK0009391021 | 1 JYK E RTL 2023 | 2023-04-01 | 8.68 | 3.5954 |
| DK0009796864 | 1 NYK H RTL 2023 | 2023-07-01 | 26.14 | 3,8590 |
Table 6: The largest RTL bonds for each of the five main mortgage institutes in Denmark maturing in 2023.
In a portfolio, we start out with only “1 RD T RTL 2023” and add one bond at a time distributing the invested amount in each bond uniformly. The correlation multiplier for bonds of different issuer names should reduce the CSR charge. Figure 6 shows the results. CSR capital needs decreases from 3.36 to 2.45 (approximately 27%) when moving from one to five bond issuers.
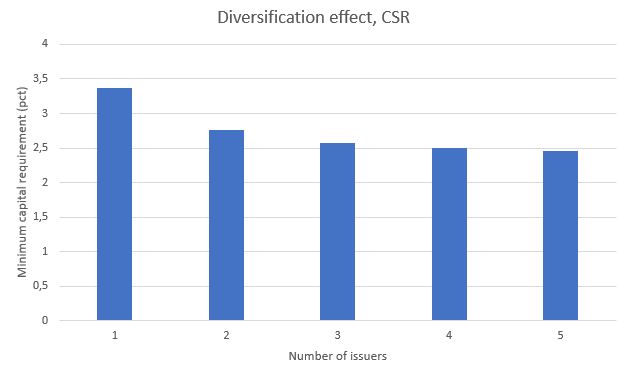
Figure 6: CSR capital charges from holding RTL bonds maturing in 2023 in the trading book. Required capital decreases when bond portfolio investments are distributed among different issuers.
Key takeaways
In this blog, we have investigated the impact of FRTB on Danish bonds in the simplest case of RTL bonds. We have explained the FRTB standardised approach framework and applied it to the largest Danish RTL bonds.
When we compare the new capital charges with existing ones, we observe a smaller capital impact than anticipated, the highest being 27% for the 10-year bonds. However, this could be due to the Danish interpretation of default risk capitalization. If we exclude the default risk component, the capital impact is very close to 40% for all RTL bonds. Either way, these numbers are not likely to cause material changes in Danish banks’ appetite for RTL bonds.
We stress the point that our results are based on single bond portfolios and that FRTB also introduces new netting possibilities for spread and default risk. We show that the CSR capital charge is reduced by approximately 27% when dividing an investment in 3Y RTL bonds into more bonds from different issuers. Also, the final impact of FRTB will depend on how the bank has hedged its positions which have not been covered in this blog.
Please contact Scanrate at support@scanrate.dk (phone +45 86 205 210) if you have questions to this topic or if you are interested in hearing about our solutions for FRTB compliance.
Footnotes:
1 The Danish bond market primarily consists of mortgage backed bonds. These are backed by a pool of mortgages, and all bonds bear a AAA-rating. There are three major types of bonds: Fixed rate non-callable bullet bonds with up to 10 years to maturity (RTL bonds), floating rate notes, and callable fixed rate bonds with up to 30 years to maturity.
2 European Parliament (2019/876) Article 325a bullet 1.
3 The shortest RTL bonds – 1Y and 2Y maturity – have an embedded option to extend if interest rates increase more than five pct. within a year. They are therefore not exempt from curvature and vega capitalization, but currently the options are very far out of the money. In the effort of writing a concise blog, these calculations are saved for later.
4https://www.scanrate.dk/blog/archive/when-do-key-rate-measures-add-up/
5 Basel (Jan 2019) 21.46
6 CSR risk buckets, risk weights and correlations are found in Basel (Jan 2019) 21.51 – 21.54
7 European Parliament (2019/876) Article 325ah
8 Basel (Jan 2019) 22.9 – 22.30
9 European Parliament (2013/575) Article 340.
References:
- Basel Committee on Banking Supervision, January 2019: Minimum capital requirements for market risk,
https://www.bis.org/bcbs/publ/d457.htm
- Basel Committee on Banking Supervision, January 2019(b): Explanatory note on the minimum capital requirements for market risk,
https://www.bis.org/bcbs/publ/d457_note.pdf
- Basel Committee on Banking Supervision, March 2018: Frequently asked questions on market risk capital requirements,
https://www.bis.org/bcbs/publ/d437.htm
- The European Parliament, June 2019: REGULATION (EU) 2019/876,
https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A32019R0876
- The European Parliament, June 2013: REGULATION (EU) 2013/575,
https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A32013R0575
- Finanstilsynet, December 2019: Vejledning om tilstrækkeligt kapitalgrundlag og solvensbehov for kreditinstitutter,
https://www.retsinformation.dk/Forms/R0710.aspx?id=211732
