In this blog series we investigate the impact of FRTB on the Danish bond market. In Scanrate (2020), we gave an overview of the standardised approach in FRTB (SA-FRTB) for bonds and analyzed the effects on capital requirements for non-callable fixed rate bonds (RTLs). In this blog, we move on to Danish floating rate mortgage bonds with and without a cap/floor. The value of floating rate notes depends on the fixing curve which is a separate risk factor in SA-FRTB.
As part of developing the Basel III framework, the Basel Committee on Banking Supervision initiated the Fundamental Review of the Trading Book (FRTB). Several years later, the outcome is a new set of global standards for calculating minimum capital requirements for market risk in the trading book. The EU plans to implement the standards for European credit institutions in the Capital Requirements Regulation/Directive (CRR/CRD) in the coming years.
Floating rate notes with no cap have grown increasingly popular for funding of mortgage loans over the past few years, and they are generally issued with a maturity less than five years. Our calculations in this blog show that capital requirements for floating rate notes are roughly unaffected by SA-FRTB compared to the current Danish legislation.
Capped floaters have become less popular as funding instruments over the past years. However, a significant number of 30-year capped floaters issued between 2004 and 2007 as well as 10-year capped floaters issued between 2014 and 2017 are still traded in the market today. The embedded cap introduces non-linearity in bond prices, which is not explicitly accounted for in the previous Basel accords. However, the new SA-FRTB regulation capitalizes the associated non-linear risks using new risk measures, curvature and vega.
We find that for mid- and long-term capped floaters, the capital increase is close to the Basel initial estimates of 40%. However, the main driver for increased capital is the increased credit spread risk weight, and not the new risk measures. This is because most embedded caps in the Danish mortgage bond market are far out of the money at the current interest rate levels. We show that if interest rates increase, curvature and vega will generate much larger capital requirements.
All results are calculated on non-hedged single bond portfolios. FRTB also introduces new netting rules and the final impact of the new framework will depend on how the bank has hedged its exposures.
You may also want to read
- An introduction to FRTB for Danish bonds
- How will FRTB affect required capital for RTL bonds?
- How will FRTB affect required capital for Danish fixed-rate callable bonds?
Setting the stage for SA-FRTB calculations
In the following sections, we provide a walk-through of SA-FRTB calculations for DKK denominated floating rate notes (FRNs), possibly with a cap and/or floor. The section is divided into the different risk measures and sub-divided into the risk classes GIRR (General Interest Rate Risk) and CSR (Credit Spread Risk).
Delta
CSR, constructing the credit spread curve
For RTL bonds, we use an issuer yield curve estimated from liquid RTL bonds to calculate CSR in Scanrate (2020). The issuer term structure is defined up until the longest running RTL bonds maturing at about 10 years. For floating rate notes, we use the bond’s option-adjusted spread (OAS) matching the latest official end-of-day quote as credit spread, i.e. in CSR-calculations the curve to shock will be the OAS parallel shifted DKKCITA curve. The credit spread curve is decomposed into five key rates which will be the risk factors of delta CSR.
GIRR, variable coupons lead to more risk factors
Compared to a fixed-rate bond, the future coupon rates of FRNs are unknown and depend on future values of the underlying reference rate, e.g. 6M CIBOR. From traded derivatives with the reference rate as underlying, such as swaps and FRAs, we may construct a term structure, e.g. a 6M CIBOR yield curve, and use it for projecting FRN coupon payments. We denote this term structure the fixing curve, which is a risk factor under GIRR in SA-FRTB.
In our calculations, we have chosen the Danish CITA-curve as the discounting curve and the fixing curve will be the tenor curve associated with the underlying reference rate. Figure 1 shows the CITA and the CIBOR6M curve on 21 October 2019.
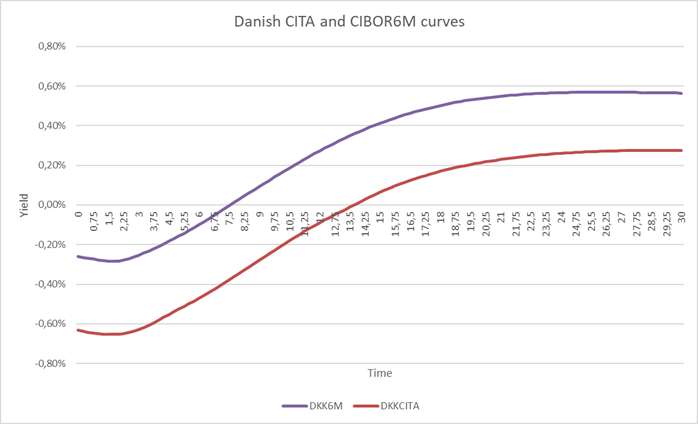
Figure 1: Danish CITA and CIBOR6M curves on 21 October 2019.
The usual way of calculating interest rate sensitivities for FRNs is to shift both curves simultaneously. However, Basel (Jan 2019) 21.8 (1c) stipulates a different approach. We need to shock both curves exclusively and the interdependency of the curves is captured using the correlation matrix with a curve correlation of 99.9%. Figure 2 shows an example of the shocks performed in the GIRR calculations.
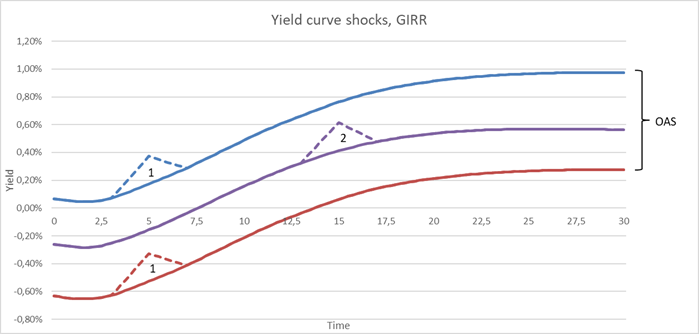
Figure 2: The yield curves are shocked in two stages. First the discounting curve (red) is shocked at all ten maturity tenors, this also affects the credit curve (blue). Then the fixing curve (purple) is shocked at all ten maturity tenors.
Like the discounting curve, the fixing curve is decomposed into ten key interest rates, so there are twenty GIRR delta risk factors for FRNs. For “NDA CIBOR6M 2023” (DK0002044478) the delta sensitivities are
| CURVE | 0.25Y | 0.5Y | 1Y | 2Y | 3Y | 5Y | 10Y | 15Y | 20Y | 30Y |
|---|---|---|---|---|---|---|---|---|---|---|
| Discounting | -0.0002 | -0.0009 | -0.0037 | -0.0074 | 2.4419 | 1.3223 | 0 | 0 | 0 | 0 |
| Fixing | 0.2017 | -0.0037 | 0.0050 | 0.0122 | -2.4252 | -1.3137 | 0 | 0 | 0 | 0 |
Table 1: GIRR delta sensitivities for ”NDA CIBOR6M 2023” on 21 October 2019. The bond is a regular floater with no embedded caps. The discounting and fixing curves have opposite effects on bond value illustrating why floaters generally have low durations.
Aggregating these 20 risk factors into a GIRR delta capital requirement requires a correlation matrix. Let \(A\) be the 10x10 correlation matrix from Basel (Jan 2019) 21.46 and \(B=0.999 \cdot A\). \(B\) now reflects how tenor points of the discounting curve is correlated to tenor points of the fixing curve, and vice versa. The combined correlation matrix has dimensions 20x20
$$C= \begin{pmatrix} A & B \\ B & A\\ \end{pmatrix}$$
In a portfolio of FRNs with a 20x1 vector, \(WS\), of weighted sensitivities, the GIRR delta capital requirement is
$$K^{Delta}_{GIRR}= \sqrt{(WS^T \cdot C \cdot WS)^+}$$
$$\qquad \qquad \quad \ = \sqrt{\Bigl(\sum_{k}\sum_{l} \rho_{k l}WS_{k}WS_{l}\Bigl)^+}$$
Price sensitivities towards discount and fixing rates
The relationship between the FRN price and discount and fixing rates, respectively, is shown in Figure 3. It shows the well-known fact that the fixing and the pricing/discounting curves have opposite effects on the price. Since the curves are closely correlated, this results in a very small GIRR sensitivity for FRNs mainly originating from the first-coming interest payment which has been fixed1. If the FRN is capped, the price-fixing rate relationship is non-linear. When the cap is in-the-money, the floating rate note will behave like a fixed-rate bond and become more sensitive to interest rate fluctuations.
The red line in Figure 3 corresponds to the CSR delta since shocking the discounting curve is equivalent to shocking the credit spread. In the CSR calculations, however, the fixing curve is not a risk factor and will therefore not negate the loss/gain from increasing/decreasing credit spreads. The holder of the FRN has the full spread risk which is why the increasing spread risk weights of SA-FRTB is the main source of the increase in reserved capital.
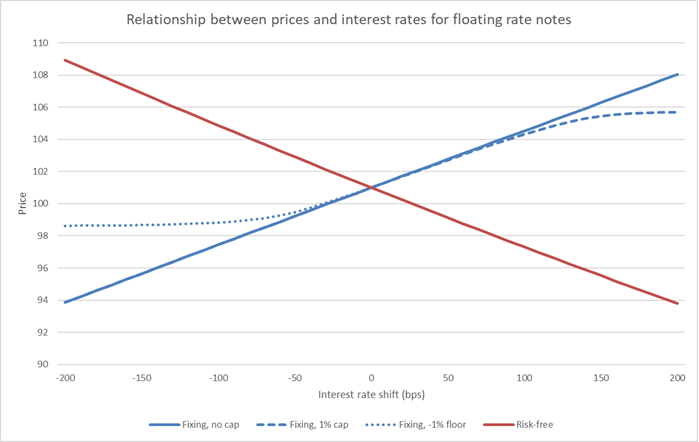
Figure 3: Relation between interest rate level and price for a Danish floating rate mortgage bond with 4 years to maturity. The blue curves represent the fixing curve while the red represents the pricing/discount curve. The opposite effects on the price results in pure floaters having next to no interest rate risk. The opposing effects of the curves weaken for capped floaters as the moneyness of the option increases.
Curvature
GIRR, capped floaters exhibit curvature risk
The non-linearity of capped floaters shown in Figure 3 will create losses in adverse interest rate scenarios not captured by the first-order risk measure, delta. Therefore, SA-FRTB introduces the curvature risk measure. The curvature calculation method is described in Basel (2019) 21.5 and we introduce the method in a Danish mortgage bond context in the fact box below.
|
Fact box - Curvature risk capital requirement To calculate the curvature risk capital requirement, we perform a full repricing of all instruments subject to curvature risk in an upward and downward scenario for the relevant risk factors. The general net curvature loss formula is
$$CVR^{up}_k=-\sum_i{\Bigl(V_i (x_k^{RW^{up}})-V_i(x_k)-RW \cdot s_{ik}\Bigr)}$$ $$CVR^{down}_k=-\sum_i\Bigl({V_i (x_k^{RW^{down}})-V_i(x_k)+RW \cdot s_{ik}\Bigr)}$$
\(V_i(x_k)\) is the value of instrument \(i\) at the current value of risk factor \(k\). \(x_k^{RW^{up/down}}\) is the risk factor shifted up or down by the risk weight \(RW\). \(s_{ik}\) is the delta sensitivity. In GIRR specifically, the risk factor \(k\) is the collapsed term structure of interest rates meaning that all curves are shifted synchronously, cf. Basel (2019) 21.8.(5). This also means that \(s_{ik}\) is the sum of the key rate sensitivities across all relevant yield curves. The curvature risk measure uses the same buckets as delta, e.g. currency. Since there is only one risk factor, the capital requirement for bucket \(b\) becomes $$K_b^{Curvature}=max(CVR^{up}_k, CVR^{down}_k, 0)$$
|
Figure 4 illustrates the curvature effect on a FRN capped at 1%.
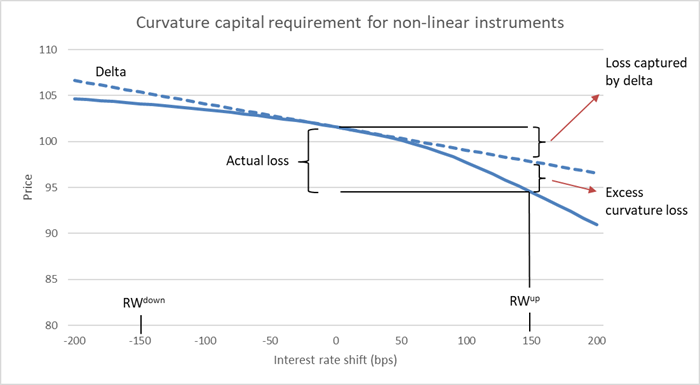
Figure 4: Price changes for a FRN with a 1% cap. All curves are shifted simultaneously according to a risk weight of 150 bps. When interest rate levels approach the cap, future coupon rates remain roughly the same, but the discount rates continue to increase causing the price decline to steepen.
CSR, no optionality on the credit spread
As there is no optionality on the credit spread, Danish mortgage bonds should not be capitalized due to curvature of credit spreads.
Vega
GIRR, the cap value depends on interest rate volatility
Like all other options, a cap depends on the volatility of the underlying. FRTB instructs that vega risk should be decomposed into a vega vector consisting of 25 ATM swaption sensitivities within the currency and combined to a capital requirement using a correlation matrix. We are still fine tuning these vega vector calculations and present vega capital numbers corresponding to a parallel shifted ATM volatility surface in this blog.
CSR, no optionality on the credit spread
As there is no optionality on the credit spread, Danish mortgage bonds should not be capitalized due to the volatility of credit spreads.
Risk factor overview
Table 2 presents an overview of risk factors associated with FRNs in SA-FRTB.
| CLASS | MEASURE | BUCKET | FACTORS | REFERENCE | MANDATORY |
|---|---|---|---|---|---|
| GIRR | Delta | Currency | Risk-free yield curves @ 0.25, 0.5, 1, 2, 3, 5, 10, 15, 20, 30Y |
21.8.(1) | All |
| CSR | Delta | Rating and sector | Issuer credit spread curve @ 0.5, 1, 3, 5, 10Y |
21.9.(1) | All |
| GIRR | Curvature | Currency | Risk-free yield curve (all curves) | 21.8.(5) | Cap |
| GIRR | Vega | Currency | Implicit volatilities of interest rate options defined along two dimensions: The maturity of the option and the maturity of the underlying, both @ 0.5, 1, 3, 5, 10Y | 21.8.(4) | Cap |
Table 2: Risk factors related to floating rate notes defined by FRTB. Reference paragraphs refer to Basel (Jan. 2019). It is only mandatory to calculate curvature and vega capital requirements for capped floaters.
It should be noted that Danish floating rate mortgage bonds can be prepayable, but borrower prepayment is generally not considered interest rate driven. Instead, prepayment is driven by non-financial motives like moving for a new job or due to a divorce. Therefore, we do not consider the prepayment option of floating rate notes to be capitalized under SA-FRTB.
So what is the effect of SA-FRTB?
In the following section, we only go through the curvature calculation which is new compared to Scanrate (2020). If the reader is not familiar with the delta and DRC calculations in SA-FRTB, we kindly refer to the previous blog.
GIRR calculation for a single capped floater mortgage bond
We use “NYK Cibor6M 3%cap 2028” (DK0009515959) to show how the calculations are performed. All calculations are performed on 21 October 2019.
The delta GIRR vector is shown in Table 3. The sensitivities are needed to calculate the curvature capital requirement.
| CURVE | KEY RATE | SENSITIVITY (\(s_k\)) | RISK WEIGHT (\(RW_{k}\)*) | WEIGHTED SENSITIVTY (\(WS_{k}\)) |
|---|---|---|---|---|
| 0.25 | 0.0001 | 1.7% / \(\sqrt{2}\) | 0.0001 | |
| 0.50 | 0.0000 | 1.7% / \(\sqrt{2}\) | 0.0000 | |
| DKKCITA | 1 | 0.0002 | 1.6% / \(\sqrt{2}\) | 0.0003 |
| (discounting) | 2 | 0.0019 | 1.3% / \(\sqrt{2}\) | 0.0017 |
| 3 | 0.0151 | 1.2% / \(\sqrt{2}\) | 0.0128 | |
| 5 | 2.3702 | 1.1% / \(\sqrt{2}\) | 1.8436 | |
| 10 | 6.5067 | 1.1% / \(\sqrt{2}\) | 5.0610 | |
| 0.25 | 0.2043 | 1.7% / \(\sqrt{2}\) | 0.2456 | |
| 0.50 | -0.0044 | 1.7% / \(\sqrt{2}\) | -0.0053 | |
| DKK CIBOR6M | 1 | 0.0014 | 1.6% / \(\sqrt{2}\) | 0.0016 |
| (fixing) | 2 | 0.0022 | 1.3% / \(\sqrt{2}\) | 0.0020 |
| 3 | -0.0042 | 1.2% / \(\sqrt{2}\) | -0.0036 | |
| 5 | -2.5414 | 1.1% / \(\sqrt{2}\) | -1.9767 | |
| 10 | -5.9852 | 1.1% / \(\sqrt{2}\) | -4.6554 |
Table 3: GIRR delta sensitivities for ”NYK Cibor6M 3%cap 2028” on 21 October 2019. The sensitivities are expressed for a 1 pct. shift size. Due to the bond maturity in 2028, key rates for maturities above ten years are zero and omitted.
The sum of the \(s_k\) vector is \(0.5669\) while GIRR delta becomes \(0.5278\) using the prescribed correlations. Beware that these are mapped bond durations which indicates losses when positive. To fit into the equation of the fact box, we must multiply it with -1 to reflect the actual slope of the price-yield-curve. That is, \(s_{ik}=-0.5669\).
The risk weight \(RW^{up/down}\) is in GIRR determined as the largest delta risk weight which is equal to \(\frac{1.7\%}{\sqrt 2}\). The first order effect in the up scenario is hence equal to \(s_{ik} \cdot RW^{up}=-0.5669\cdot \frac{1.7\%}{\sqrt2}=-0.6814\) and must be subtracted from the total loss. Table 4 shows the result in each scenario.
| TERMINSTRUKTUR | SCENARIE | RISIKOVÆGT (RW) | TAB | DELTA | NET CURVATURE |
|---|---|---|---|---|---|
| DKK | Up | 1.7% / \(\sqrt{2}\) | -0.8861 | -0.6814 | 0.2046 |
| Down | 1.7% / \(\sqrt{2}\) | 0.5559 | -0.6814 | 0.1256 |
Table 4: Calculated curvature capital requirement for ”NYK Cibor6M 3%cap 2028” on 21 October 2019.
The required capital for curvature losses is \(-(-0.8861-(-0.6814))=0.2046\) for “NYK Cibor6M 3%cap 2028”.
GIRR combined
We have calculated a parallel vega of 0.71 for the bond. The parallel vega should act as an upper boundary since there is no capital discount due to correlated risk factors. Using this vega, the total GIRR component is
$$K_{GIRR}=K_{GIRR, DKK}^{Delta}+K_{GIRR, DKK}^{Curvature}+K_{GIRR, DKK}^{Vega}$$
$$=0.5278+0.2046+0.71+1.4424 \ $$
\(K_{GIRR}\) for ”NYK Cibor6M 3%cap 2028” is substantially higher than the general interest rate capitalization of \(0.5766\) dictated by the current legislation consisting only of a first-order risk measure. The increase is mainly due to vega. The bond does not exhibit a lot of curvature because the 3% cap is far out of the money.
Impact of SA-FRTB on FRNs
We will look at a range of floating rate notes with different reference rates, with and without cap/floors and in different maturity segments. The bonds are listed in Table 5.
| ISIN | BOND NAME | REF. RATE | MATURITY | OUTST. AMOUNT | CAP | FLOOR |
|---|---|---|---|---|---|---|
| DK0004605672 | RD CIBOR6M 2021 | CIBOR6M | 2021-07-01 | 20.22 | ||
| DK0009521684 | NYK CITA6M 2023 | CITA6M | 2023-01-01 | 15.44 | ||
| DK0002044478 | NDA CIBOR6M 2023 | CIBOR6M | 2023-07-01 | 13.30 | ||
| DK0009516098 | NYK Cibor6M 1.5% 2023 | CIBOR6M | 2023-07-01 | 3.17 | 1.5% | |
| DK0009523540 | NYK Cibor6M 1% 2025 | CIBOR6M | 2025-07-01 | 0.86 | 1.0% | |
| DK0009508822 | NYK Cibor6M 4% 2026 | CIBOR6M | 2026-07-01 | 4.01 | 4.0% | |
| DK0009515959 | NYK Cibor6M 3% 2028 | CIBOR6M | 2028-07-01 | 11.08 | 3.0% | |
| DK0004717394 | TK Cibor6M 0%, 6% 2036 | CIBOR6M | 2036-10-01 | 1.20 | 6.0% | 0.0% |
| DK0009361628 | JYK Cibor6M 0%, 5% 2038 | CIBOR6M | 2038-07-01 | 2.52 | 5.0% | 0.0% |
Table 5: Danish floating rate mortgage bonds. Outstanding amount is in billion DKK.
Figure 5 shows that capital impact on FRNs are similar to what we estimated for RTL bonds. The impact on short-term bonds is not significant while long-term do experience an increment to capital requirements mainly driven by the CSR component.
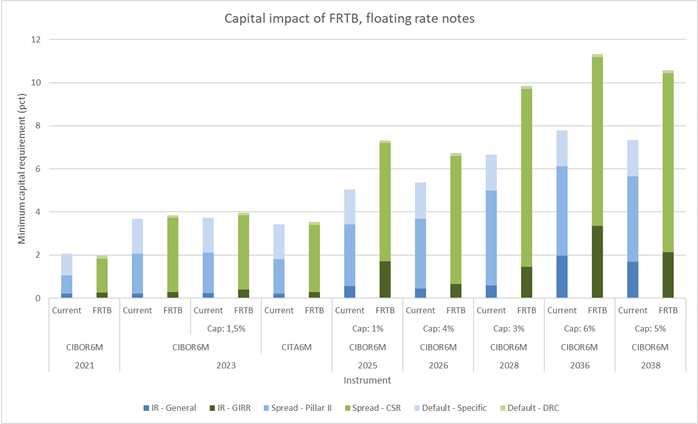
Figure 5: Estimated capital impact of Danish floating rate mortgage bonds for Danish banks. We estimate that the capital requirements stay roughly the same for short-term FRNs. The capital impact on long-term capped floaters lies around 30-40%.
The curvature part of GIRR
All caps are currently far out of the money which means that the curvature component of GIRR is rather small. Figure 6 shows the decomposed GIRR and we see that only “NYK Cibor6M 1% 2025” is subject to significant curvature risk.
The figure also shows the parallel vega effects. Especially for the long-term bonds, vega is substantial. These bonds have no curvature risk because the cap is so far out of the money, but the increase in volatility greatly affects the moneyness of the cap which lowers the value of the floating rate note.
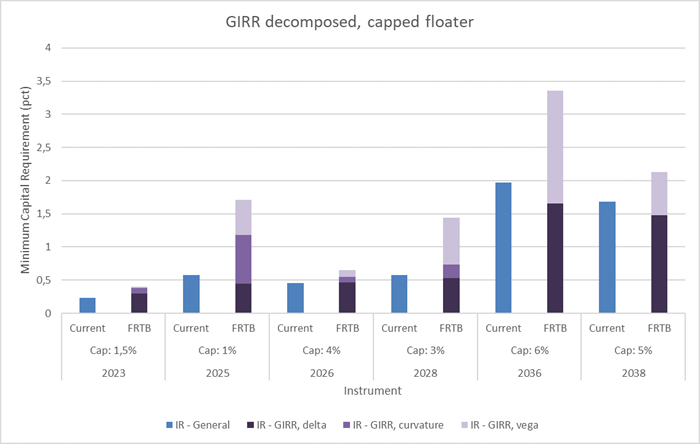
Figure 6: GIRR decomposed into delta, curvature and vega for capped floaters. The numbers are compared to current legislation. Some bonds are facing a tripling in general interest rate risk capitalization because of FRTB’s inclusion of curvature and vega risk.
The third thing to notice from Figure 6 is that the current legislation creates higher first order (delta) capital needs than FRTB for the two longest bonds. This is because the risk weights are higher in Basel II and CRR. Here, the risk weights are fixed for all tenor points on the yield curve and are solely determined by the duration (DV01) of the bond. “TK Cibor6M 0%, 6% 2036” and “JYK Cibor6M 0%, 5% 2038” have a DV01 of 2.21 and 1.88 respectively. In CRR they are assigned a risk weight of 0.85%. On the other hand, FRTB and CRR2 recognize that the shortest interest rates fluctuate the most, and the introduction of yield curve tenor risk factors enables longer tenors to be assigned with smaller risk weights. Figure 7 illustrates why general interest rate risk capital requirements are decreasing for the two longest capped floaters.
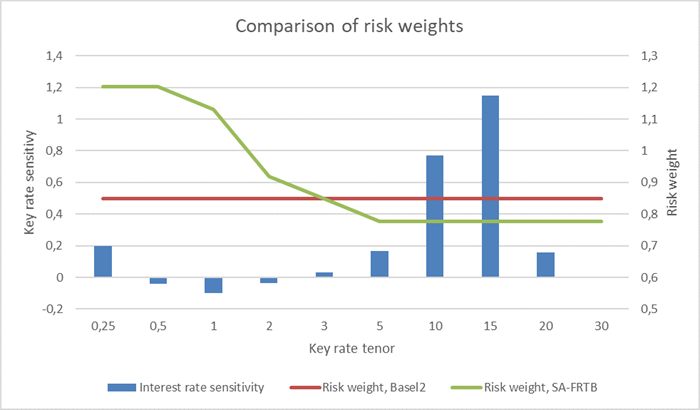
Figure 7: The capped floater “TK Cibor6M 0%, 6% 2036” is most sensitive to changes in long-term interest rates. Here, we show a regular delta vector, i.e. the fixing and pricing curves are shifted simultaneously and draw the tenor risk factors together with the delta vector. The lower risk weights for longer tenors in SA-FRTB (only in domestic and highly liquid currencies) decreases the delta capital requirements for general interest rate risk.
When the cap gets in-the-money
The conclusion thus far is that the capital requirements are not dramatically increased by SA-FRTB, but what happens if interest rates rise and the moneyness of the caps increase? To answer the question, we have studied a long-term non-callable capped floater capped at different cap values. Figure 8 illustrates that when the cap becomes more in-the-money, vega and curvature starts to increase. When the cap is deep in the money, illustrated by the 0% cap, the capped floater behaves like a fixed-rate bond and will be highly sensitive to interest rate changes as also shown in Figure 3.
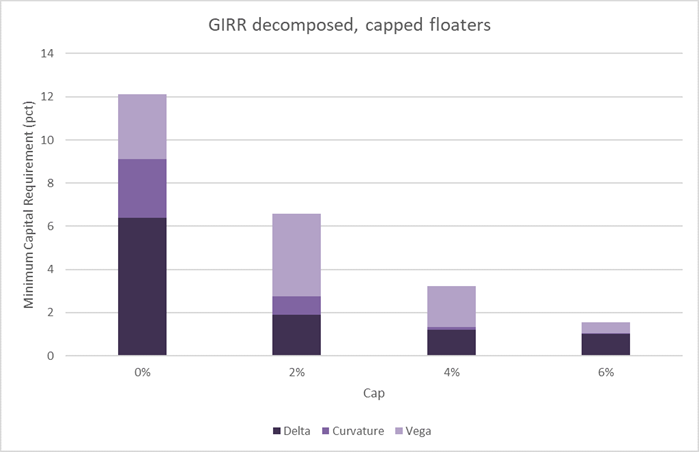
Figure 8: GIRR capital requirements for a non-callable capped floater maturing in 2038 for different cap values. When the moneyness of the cap increases so does the capital requirements.
Key takeaways
The minimum capital requirements for short-term Danish floating rate mortgage bonds are almost unaffected by SA-FRTB compared to the current Danish implementation of the rules.
Capped floaters introduce curvature risk, but at the time of writing, the caps are far out of the money, and only a couple of bonds have a significant curvature component. The capital impact on capped floaters - relative to Basel 1 - lies around 40% for the longer bonds aligning with the estimates from the Basel committee. We show that general interest rate risk capital requirements can decrease for bonds when they are sensitive to long-term interest rates, but their overall duration is low. This unexpected behavior arises because the risk weights in the current legislation are fixed across all tenors of the yield curve while SA-FRTB breaks the curve up into tenor risk factors with lower risk weights for longer tenors. We have also shown preliminary estimates of vega capital risk.
The reader is reminded that our results are based on non-hedged single bond portfolios and the final impact on SA-FRTB on Danish floating rate mortgage bonds will depend on hedging strategies.
Please contact Scanrate at support@scanrate.dk (phone +45 86 205 210) if you have questions on this topic or if you are interested in hearing about our solutions for FRTB compliance.
Footnote:
1 Unless the FRN is fixing in arrears but no Danish mortgage bonds are currently constructed that way.
References:
- Scanrate Financial Systems A/S, January 2020: Will FRTB increase required capital for RTL bonds?
https://www.scanrate.dk/blog/archive/will-frtb-increase-required-capital-for-rtl-bonds/
- Basel Committee on Banking Supervision, January 2019(b): Explanatory note on the minimum capital requirements for market risk,
https://www.bis.org/bcbs/publ/d457_note.pdf
- Basel Committee on Banking Supervision, January 2019: Minimum capital requirements for market risk,
https://www.bis.org/bcbs/publ/d457.htm
- The European Parliament, June 2019: REGULATION (EU) 2019/876, https://eur-lex.europa.eu/legal-content/EN/TXT/?
uri=CELEX%3A32019R0876
- The European Parliament, June 2013: REGULATION (EU) 2013/575, https://eur-lex.europa.eu/legal-content/EN/TXT/?
uri=CELEX%3A32013R0575