The EU's new CRD/CRR reporting requirements based on Basel's Fundamental Review of the Trading Book (FRTB) are approaching fast. This blog provides a high-level introduction to FRTB as well as the impact on capital requirements for Danish bonds. Callable fixed-rate mortgage bonds are affected the most by FRTB due to the recognition and capitalization of curvature and vega risk. The impact for non-callable bonds and floating rate notes is less significant which is probably good news for the banks.
As part of developing the Basel III framework, the Basel Committee on Banking Supervision initiated the Fundamental Review of the Trading Book (FRTB). Several years later, the outcome is a new set of global standards for calculating minimum capital requirements for market risk in the trading book. The EU plans to implement the standards for European credit institutions in the Capital Requirements Regulation/Directive (CRR/CRD) in the coming years.
Scanrate is conducting a blog series on the FRTB subject. This blog is a more general introduction to the topic while the other blogs provide detailed investigations and explanations of specific bond types.
You may also want to read
- How will FRTB affect required capital for floating rate notes?
- How will FRTB affect required capital for Danish fixed-rate callable bonds?
- How will FRTB affect required capital for RTL bonds?
The Standardised Approach
The Basel Committee has designed a set of risk calculations to assess the required capital reserves of the trading book. This is called the Standardised Approach and we denote it as SA-FRTB. The resulting capital requirement is a sum of the following components
- \(K_{SBM}\) : Capital requirement under the sensitivity-based method
- \(K_{DRC}\) : Capital requirement of default risk capital
- \(K_{RRAO}\) : Capital requirement of residual risk add on
That is $$K_{SA-FRTB}=K_{SBM}+K_{DRC}+K_{RRAO}$$
The blog focuses on \(K_{SBM}\) which is introduced below. DRC capitalizes jump-to-default risks not capitalized by credit spread shocks under SBM. RRAO captures exotic risks not included in the other two components.
The Sensitivity-based Method
SA-FRTB instructs us to calculate sensitivities to each exposure in the trading book. For bonds, two types of exposures – or risk classes – are of interest
- General Interest Rate Risk (GIRR): Recognizes that the value of a bond investment changes when market interest rates move up and down.
- Credit Spread Risk (CSR): Recognizes that the value of a bond investment changes when the creditworthiness of the issuer improves or depreciates. i.e. an idiosyncratic risk component.
In every risk class, we must calculate the sensitivities of different risk measures
- Delta measures first order changes in investment value
- Curvature captures any non-linearities, e.g. embedded options
- Vega measures volatility risk
Risk factors
The risk measures are decomposed into risk factors. E.g. the delta of a bond is decomposed into yield curves (fixing curve, risk-free curve, credit spread curve, …) and specific tenor points on those curves. In the Danish bond market, we have identified the following complete list of risk factors. Only a subset will be relevant to a given bond.
| CLASS | MEASURE | FACTORS |
|---|---|---|
| GIRR | Delta | Risk-free yield curves @ 0.25, 0.5, 1, 2, 3, 5, 10, 15, 20, 30Y Inflation curve, entire curve is one risk factor |
| CSR | Delta |
Issuer credit spread curve @ 0.5, 1, 3, 5, 10Y Borrower’s credit spread curve (refinancing curve) @ 0.5, 1, 3, 5, 10Y |
| GIRR | Curvature | Risk-free yield curves (all relevant curves are shifted simultaneously) |
| GIRR | Vega | Implicit volatilities of interest rate options defined along two dimensions: The maturity of the option and the maturity of the underlying, both @ 0.5, 1, 3, 5, 10Y |
Table 1 - Risk factors in the Danish bond market.
GIRR, delta
In all delta calculations, we must calculate the net sensitivity \(s_k\) across the relevant portfolio towards the risk factor \(k\). The net sensitivity is then converted to a weighted sensitivity \(WS_k=s_k \cdot RW_k\) where \(RW_k\) is a risk weight provided by SA-FRTB.
The GIRR delta calculation consists of regular PV01 delta vectors. For each instrument \(i\) and risk factor \(k\) the sensitivity must be calculated as
$$s_{k,i}=\frac{V_i(r_t+0.0001, cs_t) - V_i(r_t, cs_t)}{0.0001}$$
where \(r_t\) is the yield curve tenor specified by \(k\) and \(cs_t\) is a time-dependent credit spread. The net sensitivity is summed across instruments.
Certain bonds like floating rate notes depends on multiple curves, e.g. an OIS curve for discounting and a swap tenor curve for coupon fixings. In these cases, each yield curve must be shifted separately.
The risk weights for each tenor point is provided in paragraph 21.42 in the FRTB accord1 where the correlations between GIRR delta risk factors can also be found. Let \(K_{GIRR}^{Delta}\) be the delta capital requirement for the GIRR risk class and \(\rho_{kl}\) the correlation between risk factors \(k\) and \(l\).
$$K^{Delta}_{GIRR}=\sqrt{\Bigl(\sum_{k}\sum_{l} \rho_{k l}WS_{k}WS_{l}\Bigl)^+}$$
Every risk class consist of different risk buckets. In GIRR, the exposures are aggregated according to currency. The equation above only holds when GIRR exposures in the trading book are in the same currency. Furthermore, minimum capital requirements must be calculated for both low, normal and high correlation scenarios. Aggregation between risk buckets (i.e. GIRR exposures in multiple currencies) and the different correlation scenarios are not presented in this blog and the reader is referred to the official FRTB accord.
GIRR, curvature
Bonds with optionality may have significant second-order interest rate risk, i.e. curvature risk. Curvature capitalization is calculated by calculating a full repricing shift in instrument value in an upward and downward scenario less the change implied by the delta sensitivities. All curves are shifted simultaneously.
$$CVR^{up}_{k}=-\sum_i\Bigl(V_i(x_k^{RW^{up}}-V_i(x_k)-RW \cdot \overline{s_{ik}}\Bigr)$$
$$CVR^{down}_{k}=-\sum_i\Bigl(V_i(x_k^{RW^{down}}-V_i(x_k)+RW \cdot \overline{s_{ik}}\Bigr)$$
\(V_i(x_k)\) is the value of instrument \(i\) at the current value of risk factor \(k\). In GIRR, \(k\) is the risk-free yield curve. \(x^{RW^{up/down}}_k\) is the risk factor shifted up or down by the risk weight \(RW\). \(\overline{s_{ik}}\) is the sum of the delta sensitivities. The calculations are illustrated in Figure 1 using a risk weight of 150 bps.
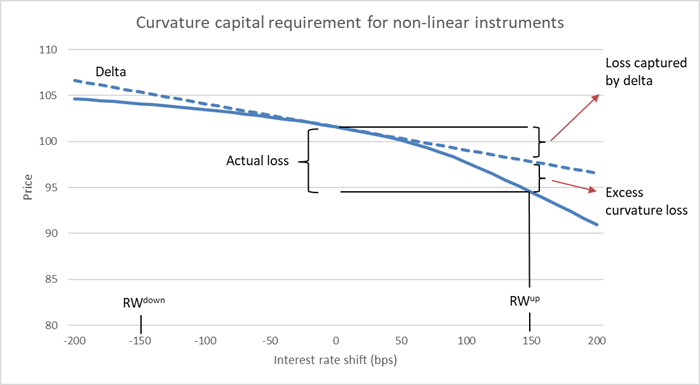
Figure 1 - Relationship between price and interest rates for a capped floater. As interest rates increase, the cap becomes more valuable and the curvature increases.
The scenario resulting in the highest capital requirement is chosen as the curvature. For a single currency GIRR exposure the capital requirement is
$$K^{Curvature}_{GIRR}=max(CVR^{up}_k, CVR^{down}_k, 0)$$
GIRR, vega
FRTB instructs that vega risk should be decomposed into a vega vector consisting of 25 ATM swaption sensitivities cf. Table 1. The sensitivity against risk factor \(k\) is the vega for instrument \(i\), \(v_{k, i}=\frac{\partial v_i}{\partial \sigma_k}\), multiplied with the implied volatility of the corresponding swaption. That is
$$s_{k, i}=v_{k, i} \cdot \sigma_k$$
At the time of writing, Scanrate is still working on selecting an optimal procedure for the allocation of the aggregate vega risk to the different swaptions and in our preliminary investigations and impact studies, we have used a parallel shifted vega as an approximation.
The vega risk factors are aggregated the same way as delta but with different risk weights and correlations.
CSR, delta
CSR captures the credit spread risk of a bond.
$$s_{k,i}=\frac{V_i(r_t+0.0001, cs_t) - V_i(r_t, cs_t)}{0.0001}$$
where \(r_t\) is the yield curve and \(cs_t\) is a time-dependent credit spread corresponding to the risk factor \(k\). We use the option-adjusted spread (OAS) as the credit spread.
The CSR risk buckets are sector and rating where most bonds in the Danish market of course fall in the covered bond risk bucket. The CSR delta sensitivities are aggregated in the same way as GIRR delta. The correlation structure is described in paragraph 21.54 of the FRTB accord where the key takeaway is that investing in different bond issuers lowers the required capital buffer2.
The capital impact of FRTB
The Basel Committee has stated that they aim for a 30-40% increase in trading book capital buffers with SA-FRTB. We have conducted a series of impact studies on single-bond portfolios and we find that fixed-rate callable bonds will be affected the most by FRTB. In the current legislation, curvature and vega risks are not addressed. Callable mortgage bonds could therefore be under-capitalized in the current regime for banks not using internal models.
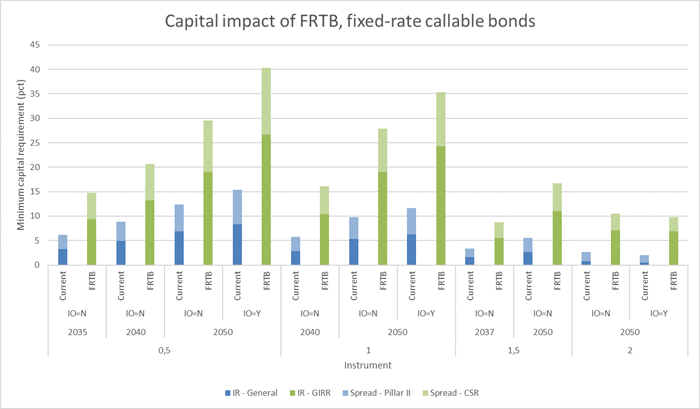
Figure 2 - Capital impact of FRTB on fixed-rate callable bonds. The new capital requirements are compared with the current CRR legislation based on earlier Basel standards. All calculations are performed on 21 October 2019.
The GIRR component is the main source of the changes. Figure 3 shows each GIRR component illustrating that the increase is caused by the new risk measures vega and curvature. Low coupon bonds have low prepayment risk and are most sensitive to volatility changes. Bonds with higher coupons have substantial prepayment risk and consequently low durations. The negative convexity of such bonds results in relatively high curvature capital requirements.
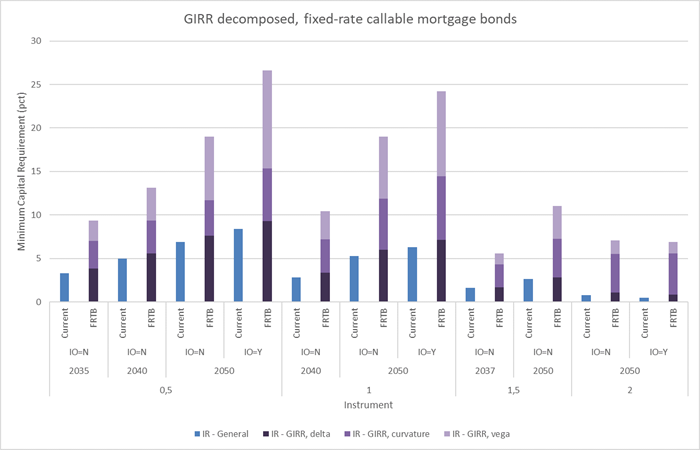
Figure 3 - GIRR decomposed into delta, curvature and vega for callables. The numbers are compared to current legislation which only considers first-order interest rate risk. All calculations are performed on 21 October 2019.
The capital impact on RTL bonds and floaters are not as remarkable. The cap option of capped floaters in the Danish market are far out of the money and regular floaters and RTL bonds have no optionality and do therefore not incorporate neither curvature nor vega risk. Figure 4 shows the capital impact for RTL bonds. The increase in capital requirements is mainly driven by the CSR component. FRTB stipulates that covered bonds must be capitalized according to a 100 bps shift in credit spreads while the current Danish legislation capitalizes mortgage bond credit risk under pillar 2 using a 50 bps shift.
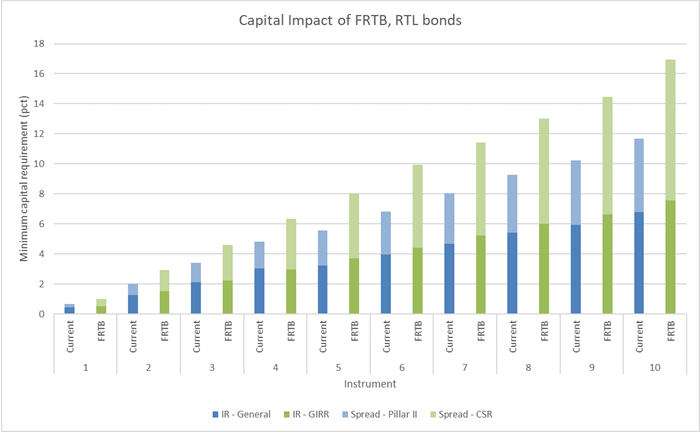
Figure 4 - Capital impact of RTL bonds across different maturities. The pillar 2 spread risk is calculated using a risk weight of 50 bps which is the minimum for mortgage bonds. Some Danish banks capitalizes mortgage bond spread risk using a higher risk weight than 50 bps. The capital impact of FRTB will be lower for those banks. The X-axis indicates years to maturity. All calculations are performed on 21 October 2019.
Key takaways
This blog provides a high-level overview of the sensitivity calculations introduced by SA-FRTB. Scanrate is able to perform said calculations with the vega vector decomposition expected to be implemented before 2020 Q4.
RTL bonds and floating rate notes are only slightly affected by the new standards, but the capital requirements for fixed-rate callable bonds will increase significantly making those instruments more expensive to hold in the trading book.
Footnotes:
1 https://www.bis.org/bcbs/publ/d457.htm
2 Also see, https://www.scanrate.dk/blog/archive/will-frtb-increase-required-capital-for-rtl-bonds/